Indhold i Matematikken formelsamlingen
Indholdet er opbygget med 12 kapitler i tre niveauer (svarende til C, B og A niveau på de gymnasiale uddannelser). Her er en oversigt over indholdet:

Det første opslag indeholder standardsymboler, koloform og indholdsfortegnelsen.

Dette opslag er indledningen til tal, mængder og algebra, dvs. om talsystemet.

Mængder, intervaller, potenser og brøker

Ligninger, uligheder, procentregning og indekstal

Kapitlet med basis geometri indledes med de basale geometri formler
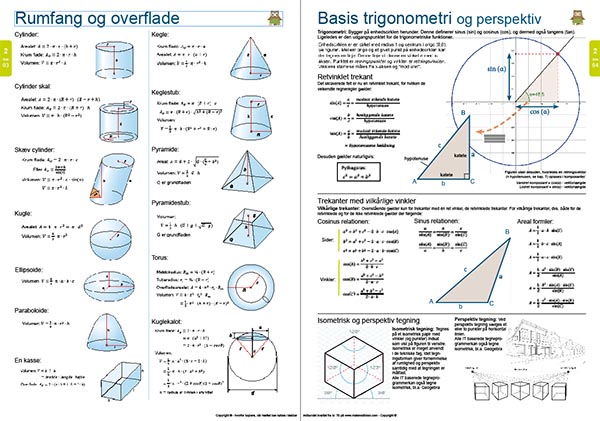
Derefter følger formlerne for rumfang og overflade samt basis trigonometri

Kapitlet med basis funktioner indledes med den lineære funktion
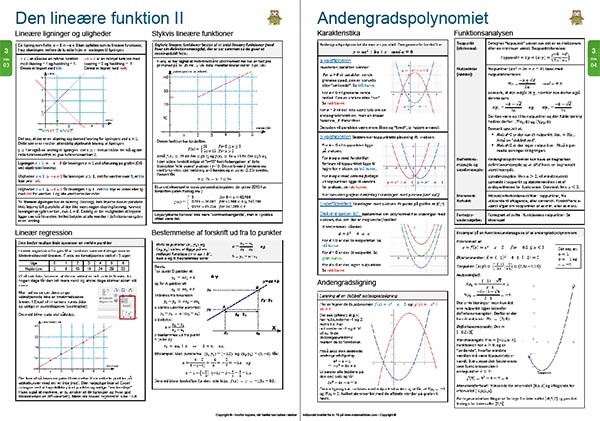
Derefter fortsættes med uddybning af den lineære funktion og andengradsfunktionen

Eksponentialfunktionen, potensfunktionen og logaritmefunktionen
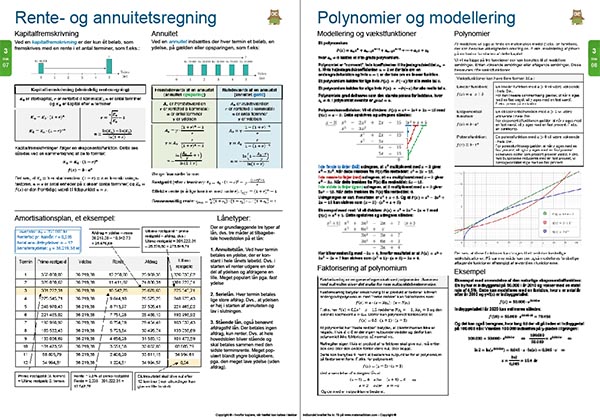
Kapitlet afsluttes med rente- og annuitetsregning samt polynomier og modellering

Big data, stikprøve og population, beskrivende, kontinuert og diskret, positionsmål, spredningsmål, trimmet gennemsnit, vejet gennemsnit, variationskoefficient, boksplot, statistiske værktøjer, diagramtyper

Diskrete og grupperede data, observationer, intervalmidtpunkt, intervalfrekvens, kvatilsæt, fraktik, variationsbredde, kvartilbredde, typeinterval, typetal, median, gennemsnit, varians, gennemsnit

Differentialer, differentiation, tangenthældning i et punkt, differentialkoefficient, grænseværdi, den afledte funktion, sekanthældningen, tangethældningen, tangetligningen

Regneregler for funktionsudtryk, regneregler for differentiering, grænseværdi, sumregel, produktregel, kvotientregel, brøkregel, potensregel
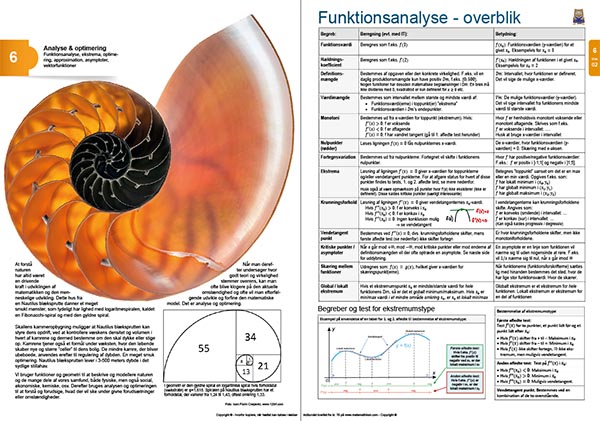
Analyse og optimering af matematiske sammenhænge, monotoni, monotoniforhold, nulpunkter, fortegnsvariation, ekstrema, krumningsforhold, vendetangent, asymptoter, skæring mellem funktioner, globalt ekstremum, lokalt ekstremum
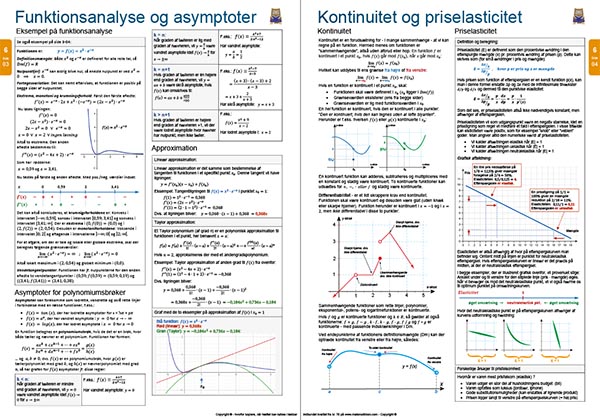
Funktionsanalyse og asymptoter, asymptoter for polynomiumsbrøker, approksimation, Taylor approksimation
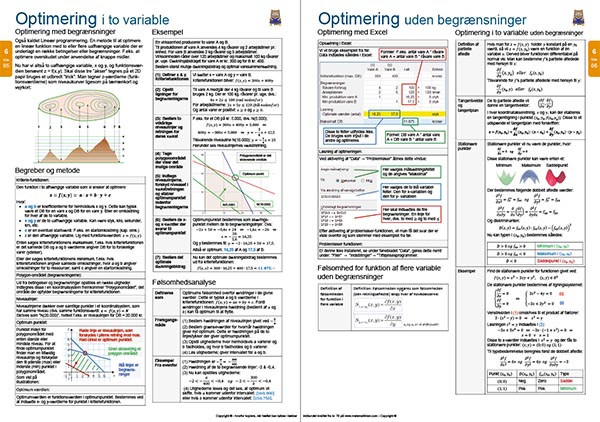
Optimering i to variable, lineær programmering, polygonområde, niveaulinjer, optimum, følsomhedsanalyse

Vektorer, regneregler og definitioner, parallelle, ortogonale, nelvektor, vektoraddition, parallelogram, multiplikation af vektor med tal, indskudsreglen, associative lov, koordinatsæt for vektorer, opløsning i komposanter, regneregler for koordinatsæt

Skalar produkt, stedvektor, tværvektor, regneregler for skalarprodukt, projektion af en vektor på en vektor, krydsprodukt, parameterfremstilling

Analytisk geometri, keglesnit, parablens ligning, hyperblens ligning

Omdrejningslegeme, om x-aksen, om y-aksen, arealmidtpunkt, massemidtpunkt

Trigonometriske funktioner, harmoniske funktioner, svingningstid, amplitude, faseforskydning, buestykke

Oversigt over differentialligninger, lineær første orden, eksponentiel vækst, logistisk vækst, inhomogen, fuldstændig løsning, partikulære løsning

Vækstfunktioner, komplekse tal, imaginære tal, kompleks form

..

..

..

..

..